(非交换)环中有一个有趣的(Kaplansky)定理说:
如果环$R$中元素$a$有不止一个右逆,那么$a$有无穷多个右逆。
这个定理告诉我们一个道理:当你错过了初恋,你就会沦为见一个爱一个的渣男0.0
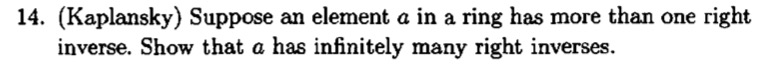
证明:(反证法)设 $a$ 的所有右逆构成的集合为 $A = \lbrace x \in A | ax=1 \rbrace $。
若 $A$ 有限,不妨设 $A = \lbrace x_1,x_2,\cdots,x_n \rbrace, (n>1)$ , 则
$$a(1- x_i a + x_1) = a-(a x_i) a + a x_1 = 1$$
并且, 若 $1- x_i a + x_1 = 1- x_j a + x_1$, 即$x_i a = x_j a$, 那么$x_i = x_i(a x_i) = (x_j a) x_i = x_j$,也就是说
$$ A = \lbrace x_1,x_2,\cdots,x_n \rbrace = \lbrace 1- x_1 a + x_1,1- x_2 a + x_1,\cdots,1- x_n a + x_1 \rbrace $$
所以存在 $k$ 使得 $ 1- a_k a + x_1 = x_1$,即 $a_k a = 1$ 所以对任意 $1 \leq i \leq n$,
$$a_i = (a_k a)a_i = a_k(a a_i) = a_k$$
即所有 $x_i$ 都相同,矛盾与 $A$ 中元素个数大于1,证毕。
等价叙述
如果环$R$中元素$a$有右逆而没有左逆,那么$a$有无穷多个右逆。